Mathematics is one of those subjects that tends to instil fear and anxiety within most children. The complex formulas, and the fear of getting it wrong, render kids nervous when solving mathematical problems. The usual methods of teaching involving solving dry and menacing numerical problems do not help much. It must be noted here that maths is one of the most critical subjects when it comes to career avenues and professional success. Students who are good at maths tend to have a plethora of lucrative career options in engineering, commerce, and management open for them. In such a scenario, how does one make sure that the kids learn maths in a manner that is fun and engaging while being devoid of any fear of failure or being judged? Puzzles seem to be the answer. Math puzzles could be a fun way to help class 3 kids master the basics of mathematics and eliminate any associated phobia. This article presents the 15 best maths-based puzzles that can be used to engage class 3 students.
Also Read: Why Studying Maths is Important for Children
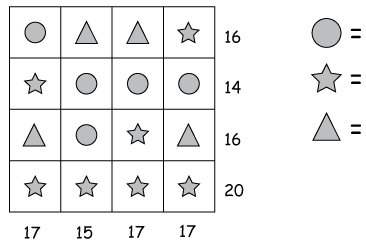
1. Mathematical operations using shapes
These puzzles associate numbers with shapes. For example,
circle + triangle + triangle + star = 16 (equation 1)
star + circle + circle + circle = 14 (equation 2)
triangle + circle + star + triangle = 16 (equation 3)
star + star + star + star = 20 (equation 4)
Find the numerical values of a circle, triangle, and star.
Solution:
From equation 4, we can conclude that 4*stars = 20, which implies, the numerical value of star = 5. We can replace this value in the other 3 equations.
circle + triangle + triangle = 11 (equation 1)
circle + circle + circle = 9 (equation 2)
triangle + circle + triangle = 11 (equation 3)
Equation 2 implies circle = 3. Replacing the value of the circle in Equation 1:
2*triangles = 8, implies triangle = 4.
The internet is full of shape-based problems that invoke a deeper sense of logic and mathematical operations for kids.
Source: mathinenglish.com
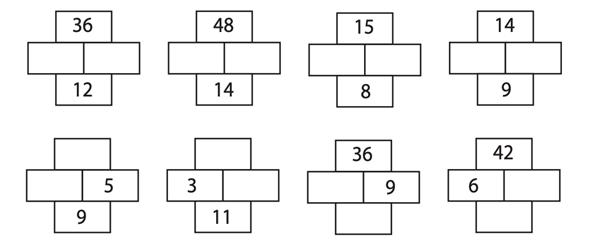
2. Product and Sum
Such puzzles expect children to find out two numbers when their sum and product are given. For example,
There are two numbers x and y. x*y = 36 and x + y = 12. Find x and y.
These puzzles can be presented in pictorial format such as the one given below where the top box is the product and the bottom box is the sum. The kids are expected to fill the empty boxes.
Source: mathinenglish.com
Also Read: 15 Hands- On Math Activities for Preschoolers
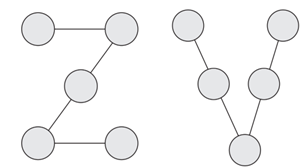
3. Number Lines
Fill in the numbers from 1 to 5 in the circles below such that each line adds up to 7 in the “Z” shape, and to 10 in the “V” shape.
Source: mathinenglish.com
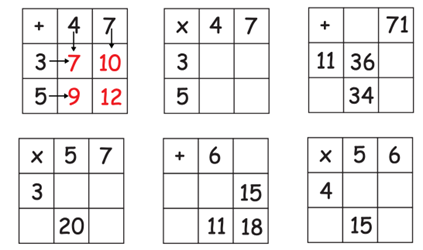
4. Number squares
Fill in the empty cells by adding or multiplying the leftmost number with the topmost number. The operation to be done is indicated by the top left cell.
Source: mathinenglish.com
5. Tree problem
Imagine 5 trees along a straight line at an equal distance from each other. The distance between the first and the 5th tree is 20 metres. What is the distance between each of the trees?
Solution:
The key to solving this problem is to understand that if there are 5 trees it means there are 5-1 = 4 gaps between them. This means that the gap between each tree is 20 / 4 = 5 metres.
The concept of this problem can be extrapolated to 100 trees with 99 gaps.
6. Train puzzles
Children are often enamoured by trains. Train puzzles could be extremely fun for them.
For example, a train comprises an engine and 10 coaches. The engine and each of the coaches are connected by a connector. The length of the engine is 25 metres, each coach is 40 metres, and each connector is 1 metre. What is the length of the train?
Solution: The key is to identify that there will be 10 connectors. Length of the train = 25 + 10*40 + 10*1 = 25+400+10 = 435 metres.
Also Read: Top 10 Ways to Utilise Maths Formulas in Day-to-Day Life
7. Missing Number
Find the missing number:
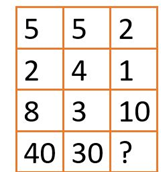
Solution: It can be noticed that the first three numbers along each column are multiplied and divided by 2 to arrive at the number in the bottommost columns. For example, 5*2*8/2 = 40, 5*4*3/2 = 30. Hence, 2*1*10/2 = 10 which is the missing number.
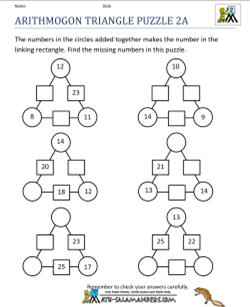
8. Triangle formation
Find the missing number. The number on the edges is the sum of the numbers on the corners.
9. Time and distance division puzzles
Sameer is driving his car at the speed of 30 kilometres per hour. How much time will he take to drive 120 kilometres?
Solution: 120/30 = 4 hours.
10. Time and distance multiplication puzzles
Arun is driving his car at the speed of 30 kilometres per hour. How much distance will he cover in 2 hours?
Solution: 30*2 = 60 kilometres.
11. Time and word puzzles
Shweta takes 3 minutes to make one chapati. How many chapatis can she make in 1 hour?
Solution: 60/3 = 20 chapatis
Also Read: Who invented Zero First: History and Facts
12. Money problems
A father distributes 140 rupees between his 3 sons. The eldest son gets double that of the middle son who gets double what the youngest son gets. How much does each son get?
Solution: Let’s assume the youngest son gets x rupees, which implies that the middle son gets 2*x rupees which implies that the eldest son gets 2*2*x rupees. The total is 140, which implies x + 2*x + 2*2*x = 140, which implies 7x = 140, or x = 20. So, the youngest son gets 20, the middle son gets 40, and the eldest son gets 80.
13. Age puzzles
The father is double the age of his son. Five years ago the father was three times the age of his son. What is the age of the father and his son as of today?
Solution: Let’s assume the age of the son is x, which implies the age of the father is 2*x. Five years ago, the age of the son would have been x-5 and the age of the father would’ve been 2x-5. So 2x-5 = 3*(x-5). Or 2x-5 = 3x-15, which means x = 10. So, the age of the son is 10 and that of the father is 20.
14. Buying groceries
Rohit goes to the market to buy some things. He has 100 rupees with him. He buys 5 chocolates at 10 rupees each, 2 pens at 20 rupees each. How much money is he left with?
Solution: 100 – 5*10 – 2*20 = 100-50-40 = 10. He is left with 10 rupees.
15. Family problems
There are two fathers and two sons. They have three apples. Each of them eats one full apple. How is it possible?
Solution: The trick here is that two fathers and two sons are not 4 people, but 3 people in total. A scenario of a son, father, and grandfather. Their combination makes them two pairs of fathers and sons. That is how they each get one apple to eat.











