The Pythagorean Theorem, a fundamental concept in geometry, has a profound impact on mathematics and its applications in the real world. Named after the ancient Greek mathematician Pythagoras, this theorem provides a simple and elegant solution to finding the lengths of sides in a right-angled triangle. In this article by EuroSchool,, we will delve into the various ways to learn the Pythagorean Theorem, its applications in real life, and present examples with solutions that showcase its versatility.
Pythagorean Theorem Formula
The Pythagorean Theorem, formulated by ancient Greek mathematician Pythagoras, states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Mathematically, it is expressed as c2=a2+b2, where c is the length of the hypotenuse, and a and b are the lengths of the other two sides. This theorem is fundamental in geometry and has widespread applications in fields such as physics, engineering, architecture, and various real-life scenarios.
Also Read: Probability: Understanding probability concepts and solving problems related to chance events.
Ways to Learn the Pythagorean Theorem
Learning the Pythagorean Theorem can be an engaging process, and there are various approaches you can take to understand and internalize the concept. Here are some effective ways to learn the Pythagorean Theorem:
Understand the Concept
- Visualise Right-Angled Triangles: Start by visualising right-angled triangles. Understand the terms like hypotenuse, base, and height. Draw triangles and label the sides to reinforce the concept.
- Real-Life Examples: Connect the theorem to real-life situations, as mentioned in the previous response. Understanding its applications can make the theorem more meaningful.
Interactive Online Resources
- Interactive Websites: Explore interactive websites and online resources that provide visualizations and interactive tools to understand the Pythagorean Theorem. Websites like Geogebra or Khan Academy offer interactive lessons.
- Educational Apps: There are numerous educational apps available for both smartphones and tablets that make learning geometry, including the Pythagorean Theorem, fun and interactive.
Videos and Animations
Educational Videos: Watch educational videos that explain the theorem visually. Platforms like YouTube have a variety of videos that use animations and demonstrations to make the concept more accessible.
Math Games
- Board Games: Play math’s board games that involve the Pythagorean Theorem. Some educational board games incorporate geometry concepts, making learning more enjoyable.
- Online Math Games: Explore online math’s games designed to teach geometry concepts. These games often present problems in a playful and interactive way.
Practical Applications
- Hands-On Activities: Engage in hands-on activities that involve measuring and constructing right-angled triangles. This can include using rulers, protractors, and compasses to enhance the understanding of geometric concepts.
- Problem Solving: Solve real-world problems using the Pythagorean Theorem. Practice applying the theorem to various scenarios to reinforce your understanding.
Classroom Instruction
- Classroom Discussions: Participate in classroom discussions to clarify any doubts and deepen your understanding. Engage with your teacher and classmates to explore different perspectives on solving problems related to the theorem.
- Practice Worksheets: Work on practice worksheets that gradually increase in complexity. Repetition and practice are key to mastering any mathematical concept.
Flashcards and Memory Aids
- Flashcards: Create flashcards with the theorem statement on one side and a visual representation or explanation on the other. Use these flashcards for quick reviews.
- Memory Aids: Develop memory aids such as mnemonics or acronyms to remember the theorem’s formula and application.
Teach Others
- Teach a Friend: Teaching someone else is a powerful way to reinforce your own understanding. Explain the theorem to a friend or family member, or even create a short presentation.
Also Read: What Is Tessellation In Geometry And How To Introduce It To Children
Application of Pythagoras Theorem in Real Life
Here are some places where the Pythagorean Theorem is applied in real life:
Architecture and Construction
The Pythagorean Theorem finds extensive application in architecture and construction. Builders use it to ensure the accuracy of right angles in structures. For example, when constructing a square corner for a building, the theorem helps measure and confirm that the diagonals are equal, maintaining the structural integrity.
Navigation and GPS Technology
In navigation and GPS systems, the Pythagorean Theorem plays a crucial role in determining distances. By applying the theorem to latitude and longitude coordinates, these technologies accurately calculate the shortest distance between two points on the Earth’s surface.
Physics and Engineering
Engineers and physicists frequently employ the Pythagorean Theorem in solving problems related to forces, vectors, and motion. Whether calculating the trajectory of a projectile or analyzing the forces acting on a structure, the theorem provides a foundational tool for these disciplines.
Medical Imaging
In the field of medical imaging, such as X-rays or MRI scans, the Pythagorean Theorem is applied to determine the distance between the source of radiation and the imaging sensor. This ensures accurate and high-quality images for medical diagnosis and treatment.
Game Development
Pythagoras’ theorem is frequently used in game development for collision detection algorithms. It helps determine if two objects in a virtual environment have collided by calculating distances between their coordinates.
Also Read: Statistics: Collecting, Organising, and Interpreting Data Through Mean, Median, and Mode
Pythagorean Theorem Examples And Solutions
Example 1: Finding the Hypotenuse:
Given a right-angled triangle with legs of lengths 3 cm and 4 cm, find the length of the hypotenuse.
Solution:
Applying the Pythagorean Theorem (a² + b² = c²):
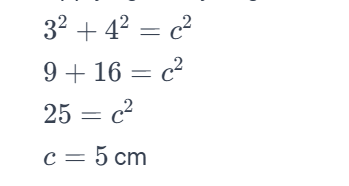
Therefore, the length of the hypotenuse is 5 cm.
Example 2: Determining a Leg Length
In a right-angled triangle with a hypotenuse of length 10 cm and one leg measuring 6 cm, find the length of the other leg.
Solution: Using the Pythagorean Theorem:
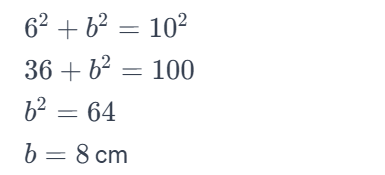
Thus, the length of the other leg is 8 cm.
Example 3: Real-Life Application – Distance between Two Points
A hiker moves 5 km east and then 12 km north. Find the straight-line distance (hypotenuse) between the starting and ending points.
Solution: Considering the hiker’s path as the legs of a right-angled triangle:
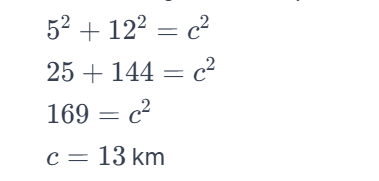
Hence, the straight-line distance between the starting and ending points is 13 km.
Also Read: Trigonometry: Introducing trigonometric ratios, trigonometric identities, and their applications
As we continue to explore and apply mathematical principles, the legacy of Pythagoras and his theorem remains an integral part of our intellectual landscape. EuroSchool employs interactive methods, real-world applications, and digital resources to make maths engaging, fostering conceptual understanding and practical skills.











