A line is a two-dimensional geometrical figure. A line can also be defined as a figure that has length but not width. A line is a key element of geometry. A combination of lines can be used to form different kinds of geometrical shapes such as a triangle with three lines, a square with four equal-sized lines, a rectangle with two longer lines and two shorter lines, and so on. This article talks about different types of lines and the role they play.
Also Read: Who invented Zero First: History and Facts
Straight line
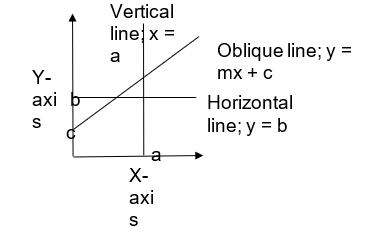
A straight line is the shortest path between any two points in space. It is represented by the equation y = mx + c in the (x, y) two-dimensional space. The slope of the line is denoted by the constant “m”. The intercept is defined as “c” which is the point where the line intersects with the y-axis, the point where x = 0.
The slope “m” determines the degree of inclination of the line. Depending on the various values of slope, straight lines can be of the following types:
– Horizontal line:
- This is a line parallel to the X-axis, which means that it has no slope or slope m = 0. The equation of such a line is y = b. Where b is the point where this line intersects the y-axis. This line will never intersect with the x-axis, until technically at infinity. The symbol hyphen “-” or underscore “_” is an example of a horizontal line.
Some examples in real life where we see horizontal lines:
- The red and white lines in the American flag
- Edges of the saffron, white and green stripes in the Indian flag
- The horizon line separating the sky from the ocean
- The lines in your English writing notebooks
– Vertical line:
- This is a line parallel to the Y-axis, which means that it has an infinite slope. The equation of such a line is x = a. Where a is the point where this line intersects the x-axis. This line will never intersect with the y-axis, until technically at infinity. The alphabet “I” is an example of a vertical line.
Some examples in real life where we see vertical lines:
- The steel fence rails in the garden
- Edges of an electricity pole
- Legs of a chair or table
- Upright trees
– Oblique line:
This is an oblique line with a non-zero slope. This line is denoted by the equation y = mx + c. Where c is the point where the line intersects with the y-axis. The obliqueness of the line is determined by the value of the slope m. The higher the value of m, the steeper the line is and the lower the value of m, the flatter the line is. The extreme cases are the vertical and horizontal lines respectively. The symbol backslash or forward slash “\” or “/” is an example of an oblique line.
Some examples in real life where we see oblique lines:
- Trees that are not upright
- The edges of the leaning tower of Pisa
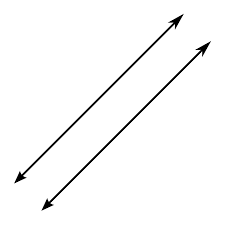
– Parallel lines:
- These are lines in the same two-dimensional plane that have the same slope “m”, but different values of “c”. These lines never intersect with each other, until infinity. Railway tracks are an example of parallel lines. The railway tracks remain at an equal distance from each other and never intersect with each other.
– Intersecting lines:
– These are lines that intersect with each other. For example, the blades of a pair of scissors. The alphabet “X” is a depiction of intersecting lines.- – – Perpendicular lines
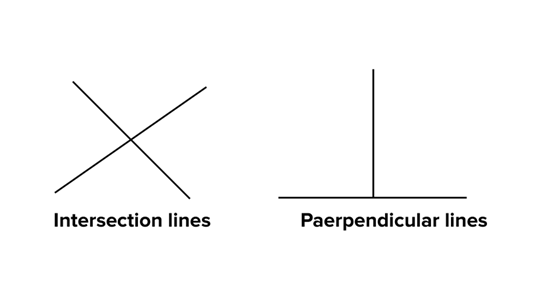
- This is a special case of intersecting lines. Two lines are perpendicular if one line has a slope of m, while the other line has a slope -(1/m). For example, the hour and minute hands of a clock at 3 o’clock and 9 o’clock are perpendicular to each other. The alphabet “L” can be seen as a combination of two perpendicular lines.
– Transversal lines.
A line intersecting two other lines at two distinct points is called a transversal line. The traditional TV antenna is an example of transversal lines. The alphabet “H” is another example of a transversal horizontal line intersecting two vertical lines.
– Concurrent lines.
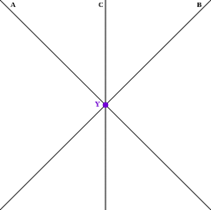
- These are two or more lines that intersect with each other at the same point.
– Skew lines
- These are lines that are not parallel to each other but still do not intersect with each other. These lines are in different planes, which is the reason why they do not intersect with each other. Imagine drawing a horizontal line on the floor and another horizontal line on the wall of your room.
– Coplanar lines
- Any two lines which are in the same two-dimensional plane are called coplanar lines.
- Curved Line. A curved line can be imagined as a line that is not straight. In other words, a curved line has a varying slope (m) as against a straight line which has a constant slope. The alphabet “C” is an example of a curved line.
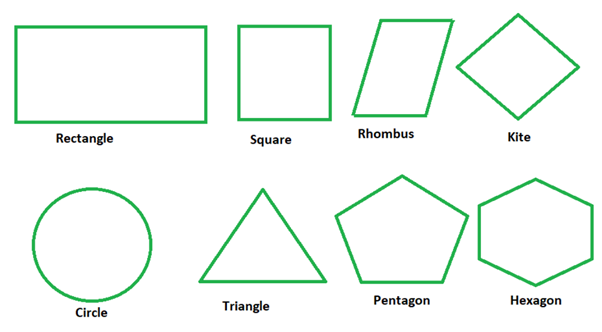
These lines in combination can be used to form geometrical shapes such as:
Triangle – one horizontal line and two oblique lines

Square – two equal horizontal lines and vertical lines

Rectangle – two equal smaller vertical lines and two equal bigger horizontal lines.
More combinations of various types of lines can be used to form a variety of geometrical shapes such as a rhombus, kite, circle, pentagon, hexagon, etc.
Also Read: Why Studying Maths is Important for Children










